fpsr

Apache License 2.0 — 详情请见 LICENSE。 Copyright (c) 2025 Woo Ker Yang (Patrick Woo) patrickwoo.1976@gmail.com 若您引用或改编此框架，请注明 Patrick Woo 及此代码仓库。 此文档仍在开发中。 尽管每次更新都旨在确保准确性，但部分内容可能仍然存在不完整或不准确之处。对此我们非常感谢您的理解，并为可能造成的任何不便表示歉意。

🎲 FPS-R: Frame-Persistent Stateless Randomisation (静态律动算法)

英文版 English README

音频简介 (英语)

一段播客风格的英语音频简介。

以下是关于后续内容的高层概述播客音频评论。

🎧 立即收听：FPS-R 与随机性的本质

引言：什么是 FPS-R？

FPS-R 是 Frame Persistent Stateless Randomisation (静态律动算法)。

FPS-R 是一个具备时间感知的伪随机数生成器，能够产生近乎不重复的模式。 给定任何递增的输入值序列（例如 frame、training-epoch、uv、latent-space、x-axis），FPS-R 会产生一个确定性的持久随机数序列。 这些数值会在变化前，以不可预测但确定的时间步长保持其值。 FPS-R 也是无状态的——它不需要在每个时间步存储状态，从而避免了复杂的逻辑和状态管理。

跨领域的 FPS-R 语法 FPS-R 中保持随机性的行为导致了以下涌现和观察到的特性：

其核心，FPS-R 是一个描述行为和现象的框架和语法，这些短语试图表达：

换言之，FPS-R 在“时间”中引入了负熵（熵的减少），注入了一种时间上的内聚力，这种内聚力在保持周期内是不规则和不均匀的。

这些是可以在多个领域观察到的普遍现象。 以下是在我们现实的各个方面发现的非线性例子，包括物理系统、社会经济系统和情感状态：

自然系统

人类系统

社会经济系统

地质/天文系统

情感的漂移与转变

fpsr_unifying_theory.md 阅读更多关于移动-保持与惊喜原则背后的思考和研究。

主要特性与效果

FPS-R 的独特结构使其产生了几种强大的涌现特性：

当前方法及其局限性

目前，模拟这种现实且复杂行为的方法有限。这些方法大多既不简单，也不方便，更不优雅。

基于 rand() 的方法

高层意图：rand()： 试图在逐帧产生跳跃输出的机制上强加结构，以期实现自然的保持周期。

如前所述，rand() 倾向于从一个种子跳到下一个种子。即使输入种子是连续的，它也无法实现连贯性的连续输出。

一个常见的解决方法是使用有状态的逻辑支架，让 rand() 在多帧内保持其值。这涉及到维护一个计数器变量，用于跟踪自上次生成随机值以来经过了多少帧。这个过程通常如下：

  1. 初始化计数器：从一个设置为零的计数器开始。
  2. 保持值：每一帧，增加计数器。
  3. 条件更新：使用 if/else 语句检查计数器是否达到预定义的阈值（保持时长）。
    • 如果达到阈值，用 rand() 生成一个新的随机值，重置计数器，并保持这个新值。
    • 如果没有，则继续保持前一个值。

伪代码示例：

hold_counter = 0
hold_duration = random.randint(min_hold, max_hold)
held_value = rand()

def get_random_value():
   global hold_counter, hold_duration, held_value
   if hold_counter >= hold_duration:
      held_value = rand()
      hold_duration = random.randint(min_hold, max_hold)
      hold_counter = 0
   hold_counter += 1
   return held_value

这种方法需要存储状态（如计数器和保持的值），并使用逻辑来决定何时“抛硬币”获取新的随机值。虽然有效，但它引入了复杂性，并需要持续的状态管理，使过程难以追踪和审计。对状态的依赖意味着每个随机流都必须记住其历史，这破坏了透明度和可预测性。

此外，有状态的方法无法轻易用于并行或分布式计算环境，包括 GPU 操作，因为在这些环境中，无状态对于可伸缩性和可复现性至关重要。随着这些有状态流的数量增加，管理它们各自状态的负担也随之增加，导致可伸缩性差和维护开销增加。

基于噪声的方法

高层意图：噪声函数： 目标是为本质上周期性且规律重复的噪声函数强加不规则性，以实现更有机和自然的随机性。

在电影、游戏和互动媒体领域，使用噪声生成随机连续性是一种常见做法。

Simplex、Perlin 等 像 Perlin 和 Simplex 这样的噪声函数在整个域上生成平滑变化的确定性输出，从而产生周期性和规则的模式。即使将这些连续梯度量化为离散步骤，其潜在的规律性仍然存在——横截面通常类似于正弦波，量化会产生可预测的、重复的过渡。这种固有的均匀性使得噪声函数无法实现具有不规则保持周期的真正随机值，因为它们的梯度是均匀分布变化的，而不是不可预测的。

Worley 或元胞噪声 Worley（元胞）噪声通过为每个点分配一个基于其与网格中最近特征点距离的值，来生成离散的、阶梯状的模式。这会产生稳定区域（保持）和突变（跳跃），但由于网格和距离计算，其底层结构仍然是规则和可预测的。虽然 Worley 噪声通过空间关系引入了复杂性，但其输出本质上是周期性的，缺乏自然时间行为所需的有机、不规则保持的随机性。因此，它无法模拟随机值不可预测的保持和变化。

当前方法、局限性与变通方案总结

对这些方法的快速回顾：

上述技术试图从规律性到不规则性的连续谱的两端来实现自然的“蓄势跳跃”行为，但最终仍未能以直观简洁的方式表达和控制自然的“动后定势”现象。

减轻噪声规律性的变通方案 为了打破规则模式，程序员和艺术家通常会引入不同、更高频率的噪声函数层，有时还进行额外的后处理，在分层和平滑之前提取“波峰和波谷”。他们还混合少量真正的随机性，例如来自 rand() 的随机性，以获得更自然的结果。

然而，这些方法本质上是相同技术的变体，继承了相同的低效率。每增加一层噪声都会增加复杂性，需要进一步的调整和参数的仔细校准。此外，每一层 rand() 都需要自己的有状态支架来管理混合和过渡，导致复杂度爆炸性提升。

这些变通方案试图通过增加复杂性来减少瑕疵，迫使原本非为此目的设计的机制以更自然和现实的方式行事。

鉴于此类结构固有的复杂性，任何修改或修订设置的尝试都需要对组件之间错综复杂的逻辑和关系有深入的理解。这种复杂性最终阻碍了表达性的探索。

数学与算法上的空缺

尽管讨论了上述各种技术，但没有一种能完全捕捉到现实世界系统中观察到的自然“蓄势后发”现象。这些方法试图从外部“强加”自然行为，通过叠加额外的过程来弥补其固有的局限性。FPS-R 直接解决了这一空缺，它从内部着手，旨在通过内在的数学原理模拟自然的“动后定势”行为，而不是依赖外部机制或支架。

FPS-R 从零开始设计，使用基于简单基础算术运算的数学和逻辑，以及一个无状态、确定性的基础，来模拟、塑造和雕刻“动后定势”的自然行为。通过避免外部支架，FPS-R 为生成不可预测但可复现的序列提供了一个干净、可伸缩且可复现的解决方案。

图解

rand() 的特征 随机数生成器 rand() 的示例输出：

[ 0.8160,
 0.9216,
 0.0572,
 0.5582,
 0.3737,
 0.4534,
 0.6260,
 0.1655,
 0.3291,
 0.5396]

每个值都与相邻值不同。这是 rand() 的目标。

FPS-R 的特征 FPS-R: QS（FPS-R 算法之一）的示例输出：

[0.9947, # jump
 0.9947,
 0.9947,
 0.4560, # jump
 0.4560,
 0.6687, # jump
 0.6687,
 0.6687,
 0.2174, # jump
 0.3755, # jump
 0.3755]

标记为 jump (跳跃) 的条目是值的变化。跳跃后的后续条目是保持的值。

这些数值和时机是不可预测的，但完全是确定性的、可复现的和无状态的。通过使用相同的参数值查找帧号，FPS-R 将始终返回相同的输出。

FPS-R的奇妙特性

奇妙的矛盾

接下来的两者是FPS-R的两个支柱，详细内容将在FPS-R的支柱部分中说明。

可预测的惊喜 FPS-R在其保持和值在时间上的跳跃方面令人惊讶，但每个时间步骤的值是完全确定性的。它只需一个递增或变化的帧编号作为输入，就能实现这种移动和保持的行为，但相同的输入帧将始终产生相同的可预测输出。

无记忆的记忆 大多数当前实现移动与保持行为的方法采用有状态技术，这些技术依赖于“记忆”（变量）来存储先前的值并为当前帧做出决策。相比之下，FPS-R的纯数学结构在不保留变量的情况下创造了记忆的假象。通过将100个帧编号输入到运行在100个独立线程上的FPS-R，并按顺序组合输出，我们观察到了一种保持和跳跃的行为。输出值似乎保持和跳跃，给人留下了记住之前状态的印象，尽管实际上没有存储变量。这一特性在并行处理环境中特别有利。

FPS-R输出的多轴特性

FPS-R的输出是一条单一的数值流。这组看似简单的数值列表实际上是一种丰富编码的结果，表达了两个随机流：

奇妙特性总结

FPS-R的确定性无状态性使得框架可重复且可检查。它的输出可完全展现在眼前，如同一个无限延伸的时间轴。我们可以“时间旅行”到任意方向，无论是向前还是向后，而无需像当前有状态的方法那样积累状态。这在模拟和可追溯审计等领域是无价的，使FPS-R具备高效和可靠的特性。

FPS-R的输出是一个丰富的多轴流，同时携带两个正交的随机轴，压缩并折叠成一条单一的流。

四种算法：SM、TM、QS 和 BD

FPS-R 包含 4 种算法。每种算法都以略微不同的方式实现移动-保持行为。

SM 叠模机制 (Stacked Modulo)

FPS-R 的节奏指纹

交互式 FPS-R 可视化工具！

这里有一个 HTML 可视化工具，用于展示四种 FPS-R 算法！ 与参数互动，实时查看输出值的更新。 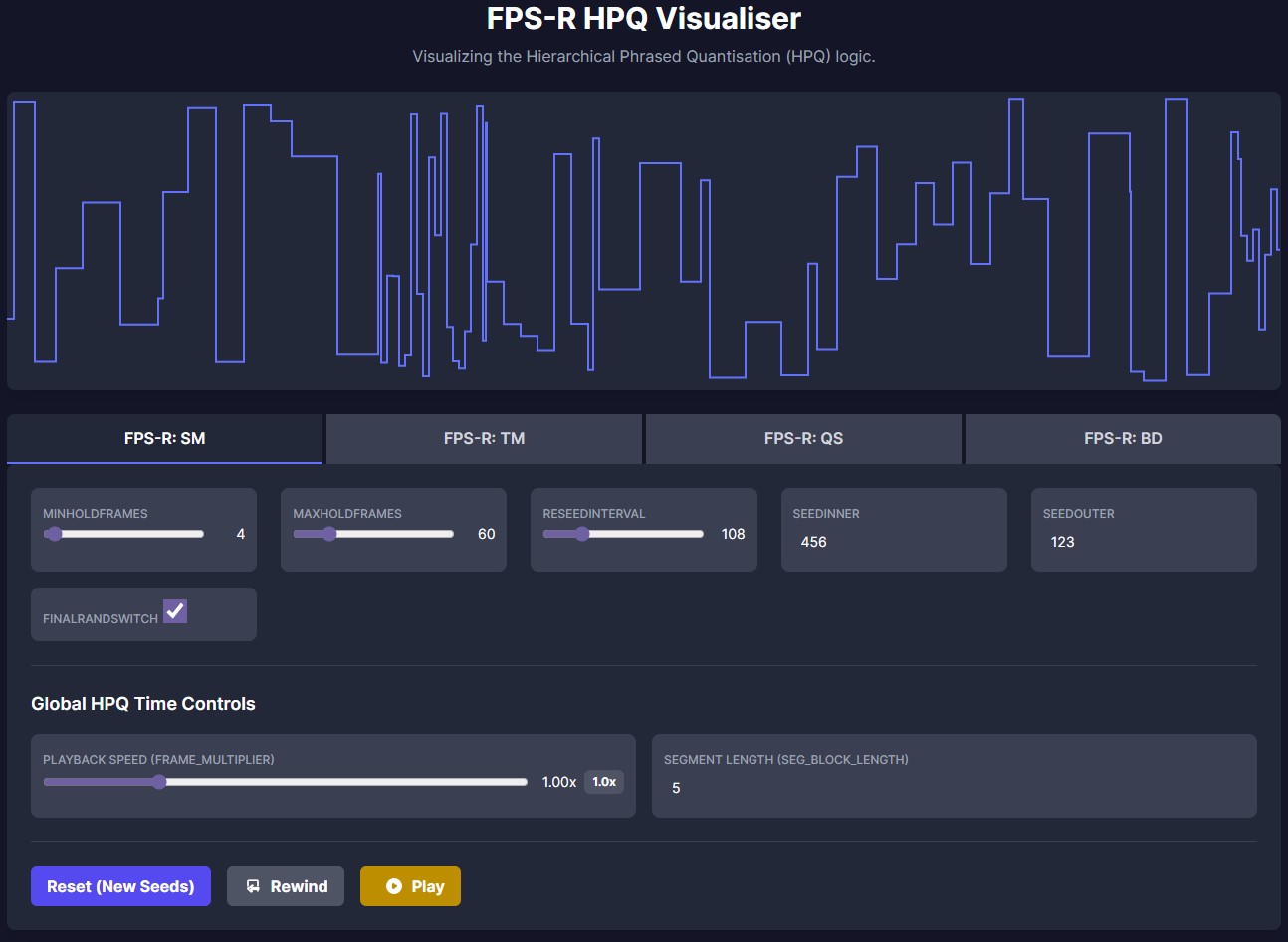点击此处查看：

FPS-R 算法可视化工具

FPS-R 算法可视化工具: 仓库中 HTML 代码

FPS-R 算法的信号分析

以下图表是 FPS-R 框架中每种算法的示例输出，运行 400 个时间步。

如何阅读图表： 蓝色实线 - 这是随时间变化的输出值。 红色虚线 - 这是 0 和 1 的值，当发生新的“跳跃”时变为 1，当值保持时回到 0。每个尖峰都是一次跳跃。

fpsr_algoAnalysis.ipynb 图表以 Jupyter notebook 的形式存在。欢迎随时探索和尝试！

如何阅读图表

FPS-R是两个折叠和压缩轴的丰富输出。它同时表达了值和时间上的随机性。

输出值图

蓝色实线 - 这些是跨时间的输出值，标准化在0.0到1.0之间。 红色虚线 - 这些是二进制0和1值。1表示一个新的“跳跃”，0表示从前一帧延续下来的值。每一个峰值都是一次跳跃。

保持步骤图

这是FPS-R中编码的“时间”轴。

保持步骤图表与时间不同步。每个数据点表示生成的随机值保持直到跳跃所经历的帧数。

portable_rand()

通过实现我们自己的伪随机数生成器，能确保结果在不同语言和操作环境中是确定性的。

portable_rand 输出值

portable_rand 这是 FPS-R 中包含的 Portable_rand() 的输出。它的工作方式非常像一般的 rand()。输入到 portable_rand() 的每一帧都会产生与前一帧截然不同的输出。没有保持数值的行为。

portable_rand 保持步骤

portable_rand 此图表不断显示1.0的步数，指示每个值到下一个跳跃值的保持帧长度为正好1帧。由于每一帧都是一次“跳跃”，每个值始终保持1帧。

portable_rand 输出时长

0.3秒可生成100,000帧。

FPS-R: SM (叠模机制)

SM 输出值

fpsr_sm 随机输出值各不相同，每个扩展的保持持续时间也不同。通过观察红色峰值之间的间距，我们可以看到不同且不规则的保持时间。时机和间距可以通过参数进行配置。

SM 保持步骤

portable_rand 此图显示了SM中每个随机值保持的帧数（或步骤）的变化。每个周期与上一个不同，表达了时间维度上的随机性。

SM 输出分布

fpsr_sm_distri 这是SM在100,000个时间步后的输出分布图。SM在经历多个时间步后可以达到均匀分布。

SM 输出时长

1.9秒可生成100,000帧。

FPS-R: TM (切换模机制)

TM 输出值

fpsr_tm 在这里，我们看到另一种看似均匀的随机值分布。在TM中，似乎存在一个潜在的节奏，交替出现三种类型的间距：大约30帧的大间距、约15帧的另一种间距以及3到5帧的短暂且不规则的间距。时机和间距可以通过参数进行配置。

TM 保持步骤

portable_rand 此图显示了TM中每个随机值保持的帧数（或步骤）的变化。每个周期与上一个不同，表达了时间维度上的随机性。

TM 输出分布

fpsr_tm_distri 这是TM在100,000个时间步后的输出分布图。TM在经历多个时间步后可以达到均匀分布。

TM 输出时长

1.6秒可生成100,000帧。

FPS-R: QS (量跃机制)

QS 输出值

fpsr_qs QS算法是FPS-R框架中第二个最具表现力的算法；能够产生广泛的短语模式，并在短暂的结巴或故障与长时间的保持之间形成最强的对比。QS拥有最多的参数。

QS 保持步骤

portable_rand 此图显示了QS中每个随机值保持的帧数（或步骤）的变化。每个周期与上一个不同，表达了时间维度上的随机性。

QS 输出分布

fpsr_qs_distri 这是QS在100,000个时间步后的输出分布图。QS的输出值分布并不均匀。这是算法的特性。分布形状（即，哪些值带会是突出且共鸣的）将根据参数的不同而有所变化。

QS 输出时长

3.2秒可生成100,000帧。

FPS-R: BD

BD 输出值

fpsr_qs BD算法是FPS-R中最具表现力的算法，得益于算法中实现参数的组合可能性。它还具有奇特的跳跃和抽搐，可能比QS更明显，因为该算法的位翻转特性。

BD 保持步骤

portable_rand 此图显示了BD中每个随机值保持的帧数（或步骤）的变化。每个周期与上一个不同，表达了时间维度上的随机性。

BD 输出分布

fpsr_qs_distri BD在100,000个时间步后的输出分布图显示出相对平坦的结果。其均匀性可与SM和TM相媲美。

BD 输出时长

3.0秒可生成100,000帧，使用1个流。 3.8秒可生成100,000帧，使用2个流。 6.2秒可生成100,000帧，使用5个流。

极大的灵活性

以上所示图表是示例输出。通过不同的参数，每种算法都可以实现各种各样的保持模式和随机值。对于FPS-R QS和FPS-R BD尤其如此。

FPS-R 的支柱

自组合性

可审计与可追踪

FPS-R 的确定性和无状态属性确保其决策易于遵循、追踪、审计和研究。

跨越多种操作环境的雄心

FPS-R 旨在跨越从计算最节俭到功能强大的高端系统的各种操作环境中使用。 轻量级 FPS-R 被设计为优化且计算轻量，甚至可以在低功耗和边缘设备上运行。但在增强的包装器版本中，输出可以扩展以在强大的高端计算环境中解锁丰富且具有分析意义的结果。 精确 包装器版本实现了比特级的精度。FPS-R 主要使用整数运算来确保精度。 在包装器版本中，浮点小数被放大为大整数以保持精度。

下面将很快详细描述具有丰富输出的增强包装器版本。

透明盒框架

由于其数学纯粹性、确定性和无状态性，FPS-R 是一个透明盒框架。其逻辑和输出是透明、可预测且无副作用的。

fpsr_manifesto.md 在此阅读更多关于 FPS-R 的宣言。

逻辑

在这 4 种算法中，SM 和 TM “比较直接简单”，但非常高效，能够生成高度表达性的输出。它们都可以用单行表达式表示。QS 和 BD 的逻辑比单行表达式所能实际表达的要复杂得多，因此它们没有“单行表达式”版本。

fpsr_tech.md 直接在此处查看每种算法的技术文档。

作为 FPS-R 一部分的 Portable_Rand portable_rand 函数是 FPS-R 的一个关键组件，它以数学上纯粹、无状态和确定性的方式，根据给定的整数种子生成一个伪随机数。

因为 portable_rand 是无状态、确定性且数学上纯粹的，任何使用它的 FPS-R 算法也将继承这些属性。

叠模机制 (SM) 的单行数学模型

为简洁起见，本文仅展示 FPS-R SM 的逻辑和表达式。 \(S_H(t) = \text{rand}\left( (t + O_o) - \left( (t + O_o) \pmod{ \lfloor H_{min} + \text{rand}(O_i + \lfloor \frac{t}{P_r} \rfloor \cdot P_r) \cdot (H_{max} - H_{min}) \rfloor } \right) \right)\) 其中:

代码中的单行表达式

让我们来看一下 FPS-R: SM 的单行表达式。

# The FPS-R:SM expression
frame = 100  # Is the current frame value
minHoldFrames = 16  # probable minimum held period
maxHoldFrames = 24  # maximum held period before cycling
reseedFrames = 9  # inner mod cycle timing
seedInner = -41  # offsets the inner frame
seedOuter = 23  # offsets the outer frame

fpsr_sm_expression = portable_rand(
    (seedOuter + frame) - ((seedOuter + frame) % (
        minHoldFrames + int(
            portable_rand(
                (seedInner + frame) - ((seedInner + frame) % reseedFrames)
            ) * (maxHoldFrames - minHoldFrames)
        )
    ))
)

代码作为函数

每个算法也被表达为一个函数，使其能够与父系统灵活交互并生成更丰富的输出。

具有丰富输出的包装版本

这些算法有“包装版本”，拥有丰富的输出结构，能够生成更深刻、有意义、分析性的输出，计算成本更高。这些特性按照细节级别（LOD）从0（最低计算成本）到2（最高计算成本）进行组织。设置一个LOD将启用与该LOD相关的丰富输出集。

帧乘数

这是所有LOD级别都可用的重要包装级特性。为了实现输出值的逐位确定性和准确性，设计上投入了大量的工作和思考。

frame_multiplier特性基于一种称为分层短语量化（HPQ）的“拉伸与生成”模型。该模型巧妙地将时间线分为两种模式，以处理时间缩放：

  1. “带速可调”（锚点）模式：当时间被拉伸（例如，frame_multiplier < 1.0）时，算法会在拉伸期间重复来自原始“内容时间线”的值。这就像放慢磁带：音高/值被保持，但持续时间更长。
  2. “望远镜扩展”（生成短语）模式：HPQ模型有一个“跑道”参数（seg_block_length），定义了该拉伸的阈值。如果时间拉伸太极端，以至于超过了这个跑道，算法将切换模式。它会停止拉伸原始值，而是生成一段新的独特随机值短语来填补空白。

优化的设计使得即使在需要生成和插入更多帧的非常低速下，其成本几乎可以忽略不计，这些帧位于常规的“实时主帧”之间。

这种双模式系统确保了慢动作在开始时感觉自然且“粘性”十足，但通过在极端时间拉伸期间引入新的、确定性生成的内容，避免了变得静态和无趣。

LOD 系统和特性

广义上，这些信息包括：

LOD 2的搜索特性 - 时间旅行

LOD 2的更高计算成本是由于其强大的无状态搜索。通过“穿越时间进行搜索”的过程是逐步向前查看以找到next_changed_frame和last_changed_frame。

为此，包装器执行两阶段搜索（先进行指数探测，然后进行二分搜索），通过递归调用LOD 0的基础算法。这种无状态的“探索”方法保证了准确性而不依赖于记忆或状态，但需要重新计算周围帧的值。

获取next_changed_frame和last_changed_frame可以解锁以下内容：

包装版本结论

这些增强功能使FPS-R的输出能够进行有意义的分析，从而实现透明度、可追溯性和可审计的工作流程。

fpsr_tech.md 在此阅读有关每个算法的技术细节。

应用领域

FPS-R 描述了一个在许多领域中发现的基本和可观察现象。因此，它几乎可以应用于任何领域，以注入复杂性和非线性。

fpsr_applications.md 更全面的文档，详细说明潜在的应用领域。

fpsr_applications.md 更全面的文档，详细说明潜在的应用领域。

未来扩展：胶囊

胶囊作为 FPS-R 的构建块

胶囊是一个自包含的、可移植的数据结构，封装了完整的 FPS-R “表现”。可以将其视为预设或片段。每个胶囊存储：

本质上，胶囊是一个单一的、可重用的“块”，具有确定性和非线性行为，存储类似于音频或视频片段的“预设”和“表现”。

这就是胶囊的强大之处。如果一个胶囊是一个“单词”或一个音乐“音符”，那么你可以将它们排列起来，创造复杂的作品。

时间线：胶囊可以按顺序放置在“时间线”或“播放列表”上。通过将不同的胶囊串联在一起——例如 cautious_hesitation.cap 后接 erratic_burst.cap——你可以为 AI、机器人或动画构建复杂的行为叙事。

真正的语法：这个系统将 FPS-R 从一个原始生成器转变为一个真正的组合语言。你不再只是雕刻一个单一的、连续的流；你是在将离散的想法排列成短语、句子和故事。这解锁了细致复杂甚至分层的行为。现在想象一下将单一时间线自然扩展为同时存在的多轨道、多通道时间线，片段并行运行，互相添加和减去。这可以创造出有意义的复杂性，从而解锁更深层次的表现力。

强大的应用示例：安全性和混淆

这创建了一个强大的双因素系统。要解锁内容，攻击者不仅需要正确的胶囊序列（时间线），还需要正确的秘密偏移。这在确定性复杂性的面纱下提供了多个独立的混淆层。

无状态、确定性随机保持和跳跃的可审计、可追踪和可控表现的表现性短语的应用广泛而多样。而在其中的核心，正是FPS-R 这个基础语法。

结论

FPS-R 不仅仅是一个伪随机数流生成器；它是一个精心设计的框架，填补了混沌随机性与严格可预测性之间的关键空白。通过提供一种无状态、确定性和数学纯粹的方式来建模自然界中发现的“保持与跳跃”现象，它为广泛的应用提供了一个新的基础原语。

除了作为一个技术原语，FPS-R 还是观察、表达和组合我们非线性世界语法的新视角。

从构建更可信的 AI 和弹性系统，到使用胶囊构建复杂的安全协议，FPS-R 提供了超越简单仿真、迈向真实、表现性组合的工具。它是一个“透明盒”框架，旨在实现探索、精确和可扩展性，邀请开发者、研究人员和创作者利用可预测的不可预测性的力量。

组合性的潜力使得 FPS-R 能够以多种方式组合其时间短语输出。展望未来，胶囊的愿景允许封装捕捉不同“情绪”的性能片段，跨越无限时间线，利用各种参数组合。这进一步解锁了更丰富且具有深度的‘蓄势跳跃’短语，使一种新的表现形式得以实现，能够与真正的非线性进行交流。

让我们一起探索 FPS-R 的无限可能性，用创意塑造非线性组合的未来！

其他文档

补充文档参考。

fpsr_tech.md 技术文档，展示所有算法的数学逻辑和代码。

fpsr_applications.md 更全面的文档，详细说明潜在的应用领域。

fpsr_unifying_theory.md 对惊奇的哲学探索，考察自然的复杂性和非线性，以及 FPS-R 如何捕捉这一本质，以增强模拟和仿真中的自然复杂性。

Origins, Journals and Reflections 起源、日志和反思 - 我开发旅程的记录，包括沿途遇到的灵感和挑战。

fpsr_algoAnalysis.ipynb 一个包含数据图表的 Jupyter 笔记本，供互动探索和实验使用。自己试试看吧！

README 英文版.

This site is open source. Improve this page.