fpsr

Apache License 2.0—see LICENSE for details.
Copyright (c) 2025 Woo Ker Yang (Patrick Woo) patrickwoo.1976@gmail.com
If you reference or adapt this framework, please credit Patrick Woo and this repository.
This documentation is still in development.
While every update aims for accuracy, some parts may still be incomplete or contain inaccuracies. I appreciate your understanding in this matter, and we apologize for any inconvenience this may cause.

🎲 FPS-R: Frame-Persistent Stateless Randomisation

中文版	Chinese README

---

An Audio Introduction: Podcast-Style

A Podcast Style Audio Introduction

Here is a high-level podcast audio commentary of the following content.

🎧 Listen Now: FPS-R and the Nature of Random

---

Introduction: What is FPS-R?

FPS-R is Frame Persistent Stateless Randomisation.

FPS-R is a time-aware pseudo-random number generator that produces practically non-repeating patterns.
Given any series of incrementing input values (e.g., frame, training-epoch, uv, latent-space, x-axis), FPS-R produces a persistent sequence of deterministic random numbers.
These numbers hold their values for unpredictable, yet deterministic time steps before changing.
FPS-R is also stateless—it does not need to store state at each time-step, which avoids complex logic and state management.

The Grammar of FPS-R Across Domains The behaviour of held-randomness in FPS-R leads to the following emergent and observed properties:

• deliberation, hesitation, intentionality
• evoked feelings of unexpected surprise and being startled

At the core, FPS-R is a framework and a grammar that describes a behaviour and phenomenon that these phrases try to express:

• hold-then-break
• move and hold
• hold and jump

In other words, FPS-R reduces entropy over time by adding temporal cohesion through irregular, non-uniform hold periods.

These are pervasive phenomena that can be observed across domains. Here are a few examples of non-linearity found in various aspects of our reality, including physical systems, socio-economic systems, and emotional states:

Natural Systems

• Flock Migration Trajectories: The movement patterns of birds or fish often show non-linear dynamics, which result from interactions among individuals and environmental factors.
• Predatory Movement: Predators and prey often alternate between holding their positions and making sudden bursts of speed during the chase and escape process.
• Quantum Particle Jumps: In quantum mechanics, particles often exhibit non-linear behaviour by suddenly ‘jumping’ from one position to another.

Human Systems

• Eye Saccades: The rapid movements of the eye exhibiting non-linear patterns in visual attention.
• Growth Rates in Organisations: The growth of organisations often follows non-linear paths, shaped by a variety of unpredictable influences.
• Product Development Speeds: The pace of innovation can vary dramatically depending on market conditions, technology, and consumer behaviour.

Socio-Economic Systems

• Financial Market Crashes: Market dynamics are often non-linear. Small changes can lead to rapid and significant chain reactions, resulting in crashes.
• Economic Growth Models: Rapid policy shifts after long periods of debates and deliberation among opposing parties, perhaps caused by small changes and accumulated tensions.
• Employment Maket: Relatively rapid increase or shrinking of jobs based on various factors such as shifts in political stability, establishing of govenment incentives and passing of immigration laws.

Geology/Astronomical Systems

• Plate Tectonic Movements: Stress gradually builds up in tectonic activities and is then released suddenly and violently during earthquakes.
• Planetary Collapses: Gravitational instability over time can result in the sudden, rapid collapse of planets and stars. This process may sometimes lead to the formation of black holes.

Emotional Drifts and Shifts

• Building Anger to Outburst: Anger often accumulates relatively slowly over time due to various triggers, building up to a final, often sudden trigger the leads to a sudden outburst.
• Hesitation to Sudden Courage: Prolonged hesitation may suddenly shift to courageous action.
• Learning and Internalising to Moments of Understanding: Learning is non-linear, where individuals may struggle for a time before achieving clarity.

fpsr_unifying_theory.md Read more about the thoughts and research behind the principle of move-hold and surprise.

Key Properties and Effects

The framework’s core design produces several distinct and powerful advantages:

• Generates Practically Non-Repeating Patterns. The layered, compositional nature of FPS-R produces complex, long-form patterns that are practically non-repeating, making it an ideal source for organic and unpredictable procedural logic.
• Resists Pattern Detection. Its inherent complexity makes its output difficult to predict, offering significant advantages in security, procedural generation, and high-fidelity simulations where avoiding predictable cycles is critical.
• Creates Emergent ‘Surprise’. By breaking predictable rhythms with irregularly held values, FPS-R generates moments of surprise and hesitation. This is key to creating behaviors that feel more natural and intentional, from AI decision-making to robotics and artistic animation.

Current Methods and Limitations

Currently, there are limited methods to emulate this realistic and complex behaviour. Most of these methods are neither simple, convenient nor elegant.

rand()-based Methods

High-Level Intent: rand(): To force structure onto a mechanism that produce actively jumping outputs from frame to frame, in an attempt to achieve naturalistic periods of holds.

As mentioned, rand() tends to jump values from one seed to the next. It cannot achieve a continuous output even when the input seeds are continuous.

A common workaround to make rand() hold its value across frames is to use a stateful logic scaffolding. This involves maintaining a counter variable that tracks how many frames have passed since the last random value was generated. The process typically looks like this:

1. Initialise a Counter: Start with a counter set to zero.
2. Hold Value: For each frame, increment the counter.
3. Conditional Update: Use an if/else statement to check if the counter has reached a predefined threshold (the hold duration).
   • If the threshold is reached, generate a new random value with rand(), reset the counter, and hold this new value.
   • If not, continue holding the previous value.

Example pseudocode:

hold_counter = 0
hold_duration = random.randint(min_hold, max_hold)
held_value = rand()

def get_random_value():
   global hold_counter, hold_duration, held_value
   if hold_counter >= hold_duration:
      held_value = rand()
      hold_duration = random.randint(min_hold, max_hold)
      hold_counter = 0
   hold_counter += 1
   return held_value

This approach requires storing state (such as counters and held values) and using logic to decide when to “toss the coin” for a new random value. While effective, it introduces complexity and demands ongoing state management, making the process difficult to trace and audit. The reliance on state means that each random stream must remember its history, which undermines transparency and predictability.

Furthermore, stateful methods cannot be easily used in parallel or distributed computing environments, including GPU operations, where statelessness is essential for scalability and reproducibility. As the number of these stateful streams increases, so does the burden of managing their individual states, leading to poor scalability and increased maintenance overhead.

Noise-based Methods

High-Level Intent: Noise Functions: The goal is to force irregularity into noise functions that are fundamentally periodic and regularly repeating, in order to achieve more organic and natural randomness.

In the world of film, games and interactive media, using noise to generate random continuity is a common practice.

Simplex, Perlin, etc Noise functions like Perlin and Simplex generate smoothly varying, deterministic outputs across a domain, resulting in periodic and regular patterns. Even when these continuous gradients are quantised into discrete steps, the underlying regularity remains—cross-sections often resemble sine waves, and quantisation produces predictable, repeating transitions. This inherent evenness prevents noise functions from achieving truly random values with irregularly held periods, as their gradients distribute changes uniformly rather than unpredictably.

Worley or Cellular Noise Worley (cellular) noise generates discrete, stepped patterns by assigning each point a value based on its distance to the nearest feature in a grid. This produces regions of stability (holds) and abrupt transitions (jumps), but the underlying structure remains regular and predictable due to the grid and distance calculations. While Worley noise introduces complexity through spatial relationships, its output is fundamentally periodic and lacks the organic, irregularly held randomness needed for naturalistic temporal behaviours. Thus, it cannot emulate the unpredictable holding changing of random values.

Summary of Current Methods, Limitations and Workarounds

A quick review of these methods:

• random number generators are too irregular - programmers have to find ways to hold their values across frames.
• noise functions are too regular - programmers and artists often have to find ways to introduce irregularity.

The techniques described above try to achieve naturalistic “hold and jump” behaviour from opposite ends of the regularity-to-irregularity spectrum, but ultimately still fall short being able to express and control the natural “move and hold” phenomenon with intuitive ease.

Workarounds to Mitigate Noise Regularity To disrupt regular patterns, programmers and artists often introduce layers of different, higher-frequency noise functions, sometimes with additional post-processing to extract “peaks and troughs” before layering and smoothing them out. They also blend in small amounts of true randomness, such as from rand(), to achieve more natural results.

However, these methods are essentially variations of the same techniques, inheriting the same inefficiencies. Each new layer of noise adds complexity, necessitating further tweaks and careful adjustments of parameters. Additionally, every layer of rand() requires its own stateful scaffolding to manage blending and transitions, leading to a complexity explosion.

These workarounds attempt to reduce artifacts by increasing complexity, forcing mechanisms originally not designed for this purpose to behave in a more natural and realistic way.

Given the complexity inherent in such structures, any attempts to modify or revise the setup necessitate a deep understanding of the intricate logic and relationships among the components. This complexity ultimately hinders expressive exploration.

A Mathematical and Algorithmic Gap

Despite the variety of techniques discussed above, none fully capture the naturalistic “hold and jump” phenomenon observed in real-world systems. These approaches attempt to “force” naturalistic behavior from the outside, layering additional processes to compensate for their inherent limitations. FPS-R directly addresses this gap by working from the inside, designed to emulate natural “move and hold” behavior through intrinsic mathematical principles rather than relying on external mechanisms or scaffolding.

Designed from the ground up, FPS-R uses mathematics and logic based on simple and fundamental arithmetic operations and a stateless, deterministic foundation to emulate, shape, and sculpt the natural behavior of “move and hold.” By avoiding external scaffolding, FPS-R provides a clean, scalable, and reproducible solution for generating unpredictable yet repeatable sequences.

---

An Illustration

The Profile of rand() Example output of a random number generator rand():

[ 0.8160,
 0.9216,
 0.0572,
 0.5582,
 0.3737,
 0.4534,
 0.6260,
 0.1655,
 0.3291,
 0.5396]

Every value is different from neighbouring ones. This is the objective of rand().

The Profile of FPS-R Example output of FPS-R: QS (one of the FPS-R algorithms):

[0.9947, # jump
 0.9947,
 0.9947,
 0.4560, # jump
 0.4560,
 0.6687, # jump
 0.6687,
 0.6687,
 0.2174, # jump
 0.3755, # jump
 0.3755]

The entries marked jump are changes in values. Subsequent entries after the jumps are held-values.

These numbers and timing are unpredictable but totally deterministic, repeatable and stateless. By looking up the frame number with the same parameter values, FPS-R will always return the same output.

The Curious Properties of FPS-R

The Curious Contradictions

The following are 2 of the pillars of FPS-R. They will be detailed in the Pillars of FPS-R section.

Predictable Surprise FPS-R is surpising in its values that hold and jump across time, but the value at each time step is perfectly deterministic. It only needs an incrementing or changing frame number as an input to achieve this move-and-hold behaviour, but the same input frame will always yield the same predictable output.

Remembering Without Memory Most current methods for achieving a move-and-hold behavior utilise stateful techniques, relying on “memory” (variables) to store and maintain previous values, using the previous value state to make decisions on the current frame. In contrast, FPS-R’s purely mathematical construct creates the illusion of memory without retaining variables over time. By inputting 100 frame numbers into FPS-R running on 100 separate threads and assembling the outputs sequentially, we observe a hold-and-jump behavior. The output values appear to hold and jump, giving the impression of remembering previous states, despite lacking any stored variables. This characteristic is highly advantageous in parallel processing environments.

The Curious Multi-Axial Nature of FPS-R Outputs

FPS-R output is a single stream of values. This seemingly simplistic list of values are a richly encoded result expressing two streams of randomness:

• Axis 1: Randomness in Value
  • if we ignore the repeated holding values and take only the unique values from the sample output list above, we get [0.9947, 0.4560, 0.6687, 0.2174, 0.3755]. This looks like what a random number generator returns when we call it 5 times sequentially.

  Here is a sample line of Python code to generate 5 random numbers from 0 to 1:

  # Generate a list of 5 random numbers, truncated to 2 decimal places
  [float(f'{random.random():.4f}') for x in range(5)]
  result: [0.9362, 0.007, 0.3853, 0.8503, 0.1027]
  

  The output shows the same kind of random, discontinuous values like our sample output above.

• Axis 2: Randomness in Time
  • Now if we take the holding duration of each value that holds across multiple frames, ie, 3 (for 0.9947), 2 (for 0.4560), 3 (for 0.6687), etc. We get [3, 2, 3, 1, 2].

  Here is a sample line of Python code to generate 5 random numbers from 1 to 5:

  # Generate a list of 5 random integers in the range of 1 to 5.
  [random.randint(1,5) for x in range(5)]
  # result: [3, 5, 3, 4, 1]
  

  This reflects the same patterns of randomness and value ranges reflected in our example output

Summary of Curiosities

The deterministic statelessness of FPS-R makes the framework repeatable and inspectable. Its output is laid out before us like an infinitely extending timeline. We can “time-travel” as far as we want to in either direction, forward and backwards without accumulating state like current stateful methods. This is an invaluable in areas of simulation and traceable audit. It makes FPS-R performant and reliable.

FPS-R’s output is a rich multi-axial stream that simultaneously carries 2 orthogonal axes of randomness, collapsed and folded into a single stream.

The 4 Algorithms: SM, TM, QS and BD

FPS-R consists of 3 algorithms. Each one achieves the move-and-hold behaviour in a slightly different way.

SM (Stacked Modulo)

• achieves stable integer holds through nested modulo, taming the over-enthusiastic rand()
• gives the most natural pacing and rhythm of “unpredictable” jumps in values.
• produces an even distribution of output over extended time

  TM (Toggled Modulo)

• toggles the holding behaviour between 2 “alternate timelines” of periodicty
• produces a stream of values that has a more structured undertone in its phrasing compared to SM.
• produces an even distribution of output over extended time

  QS (Quantised Switching)

• is the most lively, active, expressive and articulate of the algorithms.
• produces more prounounced holds, unpredictability and fickleness in its jumps and flickers.
• does not produce an even distribution of output values

  BD (Bitwise Decode)

• Generates complex, phrased rhythms by manipulating deterministic bitstreams directly.
• Achieves holds and jumps based on the detection of “bit flips” within combined, transformed streams.
• Offers the highest degree of structural complexity and expressive control over the phrasing “character” through combinatorial bitwise operations (shifts, rotates, logic gates, dynamic controllers).
• Supports multiple-streams mode (optional) that combine to a final bitstream through selectable bitwise operations.
• Can potentially be the most computationally intensive algorithm due to its block-based, multi-stream processing, but provides unparalleled expressive control over the emergent rhythmic structure. Complexity can be scaled.
• Distribution of output values is highly dependent on the chosen operations and parameters, generally not uniform.

The Fingerprints of FPS-R

Interactive FPS-R Visualiser!

Here is an HTML visualiser of the four FPS-R algorithms! Interact with the parameters and see the output values update in real-time. 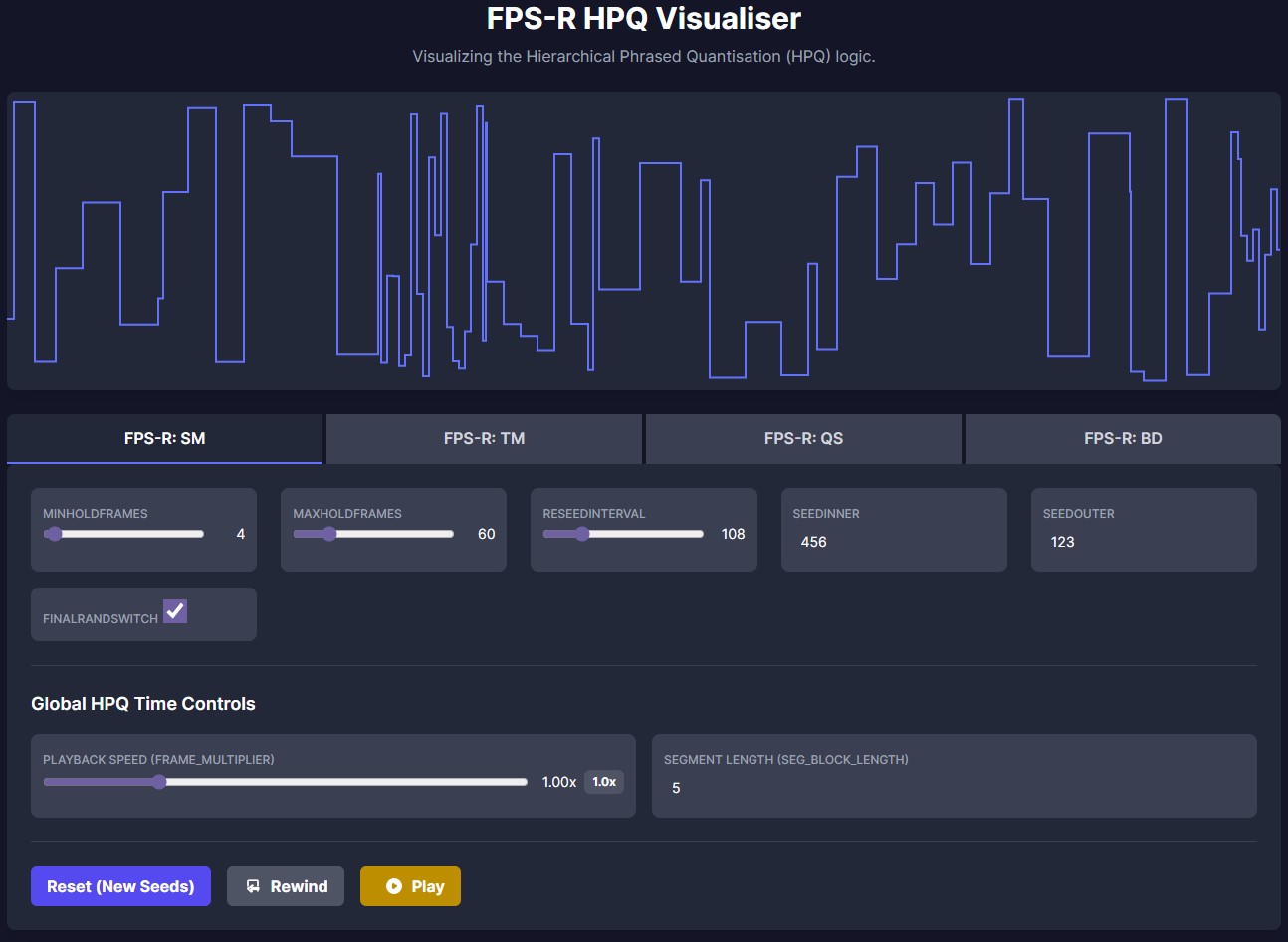Check it out here:

FPS-R Algorithms Visualiser on GitHub Pages

FPS-R Algorithms Visualiser HTML code in this repository

Signal Analysis of FPS-R Algorithms

The following graphs are sample output of each algorithm in the FPS-R framework, running for 400 time-steps.

fpsr_algoAnalysis.ipynb The following graphs exist inside a Jupyter notebook. Feel free to explore the codes and try them out!

How to Read the Graphs

FPS-R is the rich output of 2 folded and collapsed axes. It expresses randomness in both value and time.

Output Values Graphs

This is the “value” axis in the collapsed randomness.

Blue Solid Lines - These are the output values across time, normalised between 0.0 to 1.0. Red Dotted Lines - These are binary 0 and 1 values. 1 indicates a new “jump”, 0 indicates a values that is held-over from the previous frame. Every spike is a jump.

Held Steps Graphs

This is “time” axis encoded in FPS-R.

Held Steps graphs are not synced to time. Every data point expresses the number of frames that a generated random value holds until it jumps.

portable_rand()

By implementing our own pseudo random number generator, we ensure the results are deterministic across different languages and operating environments.

portable_rand Output Values

This is the output of the Portable_rand() included in FPS-R. It works very much like a rand(). Every frame input into portable_rand() yields a different output value from the previous one. Every frame is a jump with no holds.

portable_rand Held Steps

This graph is constantly showing 1.0 steps, indicating that the held frame length for each value to the next value that jumps is 1 frame exactly. Because every frame is a “jump”, every value constantly holds for 1 frame.

portable_rand Output Timing

0.3 seconds for 100,000 frames.

FPS-R: SM

SM Output Values

The random output values are varied, and their hold durations for each stretch are different. By watching the spacing between the red spikes, we can see different and irregular hold times. Timing and spacing can be configured using parameters.

SM Held Steps

This graph shows the varying number frames (or steps) that each random value holds in SM. Each period is different from the last, expressing randomness in the time dimension.

SM Output Distribution

This is the distribution graph of SM’s output after 100,000 time-steps. SM can achieve even distribution after many time-steps.

SM Output Timing

1.9 seconds for 100,000 frames.

FPS-R: TM

TM Output Values

Here we see another seemingly even distribution of random values. In TM, there appears to be an underlying rhythm, alternating between three types of spacings: a large spacing of about 30 frames, another spacing of approximately 15 frames, and a short, glitchy spacing of 3 to 5 frames. Timing and spacing are configurable through parameters.

TM Held Steps

This graph shows the varying number frames (or steps) that each random value holds in TM. Each period is different from the last, expressing randomness in the time dimension.

TM Output Distribution

This is the distribution graph of TM’s output after 100,000 time-steps. TM can achieve even distribution after many time-steps.

TM Output Timing

1.6 seconds for 100,000 frames.

FPS-R: QS

QS Output Values

The QS algorithm is the second most expressive algorithm in the FPS-R framework; able to produce a wide range of phrasing patterns and the strongest contrast between short bursts of stuttering or glitching and long periods of holding. QS has the highest number of parameters.

TM Held Steps

This graph shows the varying number frames (or steps) that each random value holds in QS. Each period is different from the last, expressing randomness in the time dimension.

QS Output Distribution

This is the distribution graph of QS’s output after 100,000 time-steps. The distribution of the output values from QS are not evenly distributed. This is the nature of the algorithm. The distribution shape (ie, which bands of values will be the prominent, resonant ones) will differ depending on the parameters.

QS Output Timing

3.2 seconds for 100,000 frames.

FPS-R: BD

BD Output Values

The BD algorithm is the most expressive FPS-R algorithm as a result of the combinatory possibilities of implemented parameters in the algorithm. It also has quirky jumps and twitches, perhaps more so than QS due to the bit-flipping nature of the algorithm.

BD Held Steps

This graph shows the varying number frames (or steps) that each random value holds in BD. Each period is different from the last, expressing randomness in the time dimension.

BD Output Distribution

The distribution graph of BD’s output after 100,000 time-steps shows a relatively flat result. The evenness is comparable to SM and TM.

BD Output Timing

3.0 seconds for 100,000 frames with 1 stream. 3.8 seconds for 100,000 frames with 2 streams. 6.2 seconds for 100,000 frames with 5 streams.

Great Flexibility

The graphs shown above are example outputs. With different parameters, each algorithm can achieve a wide variety of holding patterns and random values. This is especially true of FPS-R QS and FPS-R BD.

---

Pillars of FPS-R

• Deterministic - predictable unpredictability
  • FPS-R is predictable. While its output and timing are “unpredictable” and “surprising” in their values, holds and jumps, FPS-R always produces the same result given the same inputs (time, parameters, etc)
• Stateless - remembering without needing to know the past
  • no dependency on historical states, no need to “start from the beginning”, or to perform any run-up tasks. Pure “current frame look-up”.
  • critical for use in parallel processing environments and functional programming paradigms
• Mathematical Purity - elegant clarity in logic
  • FPS-R uses simple arithmetic operations that are well defined, well understood and do not produce side effects.
• Foundational
  • FPS-R is a construction primitive that is domain agnostic. When used together with a parent system with contextual domain logic, its output can be mapped onto any value range (continuous or discrete) and further processed to represent any number of things.
• Expressive
  • By changing parameter values, all FPS-R algorithms can achieve a wide range of expressive output patterns, invoking a similarly broad range of emergent “behaviours” and “personalities” of unpredictability and surprises. In other words, FPS-R algorithms are instruments that encourage exploration and discovery.
• Self-Composable
  • As fundamental primitives, FPS-R can be stacked onto and joined with itself or other stateless and deterministic processes, and will keep the same stateless and deterministic properties.

Auditable & Traceable

FPS-R’s deterministic and stateless properties ensure that its decisions are easy to follow, trace, audit, and study.

Ambitious

FPS-R is designed to be used across a spectrum of operating environments, from the most computationally frugal to high-powered and capable systems.

Lightweight FPS-R was designed to be optimised and computationally light, to operate even on low-power and edge devices. But in the enhanced wrapper version, output can be scaled to unlock rich and analytically meaningful results in powerful high-end computing environments.

Precise The wrapper version achieves bit-for-bit accuracy. FPS-R primarily uses integer operations to ensure precision. In the wrapper version, floating-point decimal numbers are scaled up to large integers to maintain precision.

The enhanced wrapper version with rich output will be described in greater detail shortly below.

Glass-Box Framework

FPS-R is a glass-box framework due to its mathematical purity, determinism, and statelessness. Its logic and outputs are transparent, predictable, and free from side effects.

fpsr_manifesto.md Read here for more FPS-R’s manifesto.

---

The Logic

Out of the 4 algorithms, SM and TM are “less complex” but are really efficient, delivering highly expressive output. They can each be expressed in a single-line expression. QS and BD have more complex logic than can be practically expressed in a single line, and thus do not have “single-line expression” versions.

fpsr_tech.md Go straight to the technical document of each algorithm here.

Portable_Rand as part of FPS-R The portable_rand function is a critical component of FPS-R, generating a pseudo-random number based on a given integer seed in a mathematically pure, stateless, and deterministic manner.

Because portable_rand is stateless, deterministic, and mathematically pure, any FPS-R algorithm that uses it will also inherit these properties.

Stacked Modulo (SM) One-Line Mathematical Model

For the sake of brevity this article will only show the logic and expression for FPS-R SM.

\[S_H(t) = \text{rand}\left( (t + O_o) - \left( (t + O_o) \pmod{ \lfloor H_{min} + \text{rand}(O_i + \lfloor \frac{t}{P_r} \rfloor \cdot P_r) \cdot (H_{max} - H_{min}) \rfloor } \right) \right)\]

Where:

• $S_H(t)$ is the stable float state that is held.
• $t$ is the current time or frame number (frame).
• $O_o$ is the outer seed offset (seedOuter).
• $H_{min}, H_{max}$ are the min/max hold durations (minHold, maxHold).
• $\text{rand}(seed)$ is the random number generator (portable_rand()).
• $O_i$ is the inner seed offset (seedInner).
• $P_r$ is the reseed interval (reseedInterval).

The One-Line Expression in Code

Let us take a look at FPS-R: SM in a single-line expression.

# The FPS-R:SM expression
frame = 100  # Is the current frame value
minHoldFrames = 16  # probable minimum held period
maxHoldFrames = 24  # maximum held period before cycling
reseedFrames = 9  # inner mod cycle timing
seedInner = -41  # offsets the inner frame
seedOuter = 23  # offsets the outer frame

fpsr_sm_expression = portable_rand(
    (seedOuter + frame) - ((seedOuter + frame) % (
        minHoldFrames + int(
            portable_rand(
                (seedInner + frame) - ((seedInner + frame) % reseedFrames)
            ) * (maxHoldFrames - minHoldFrames)
        )
    ))
)

The Code as a Function

Each algorithm is also expressed as a function, enabling flexible interaction with parent systems and richer outputs.

Wrapper Version with Rich Output

There are “wrapper versions” of the algorithms with rich output structures that are able to generate output that is more insightful, meaningful, analytic, at an increased computation cost. These features are organised into level-of-details (LOD) from 0 (lowest computation cost) to 2 (highest computation cost). Setting a LOD will enable the respective set of rich outputs associated with the LOD.

The Frame Multiplier

This is significant wrapper-level feature is available across all LOD levels. A lot of work and thought was put into the design to achieve bit-for-bit determinism and accuracy in the output values.

The frame_multiplier feature is built on a “stretch-and-generate” model called Hierarchical Phrased Quantisation (HPQ). This model cleverly splits the timeline into two modes to handle time scaling:

1. “Tape Varispeed” (Anchor) Mode: When time is stretched (e.g., frame_multiplier < 1.0), the algorithm will repeat the value from the original “Content Timeline” for the duration of the stretch. This is like slowing down a tape: the pitch/value is held, but it lasts longer.
2. “Telescopic Extension” (Generative Phrase) Mode: The HPQ model has a “runway” parameter (seg_block_length) that defines a threshold for this stretch. If the time-stretch is so extreme that it exceeds this runway, the algorithm switches modes. It stops stretching the original value and instead generates a new, unique phrase of random values to fill the gap.

The optimised design also results in an almost negigible costs even at very low speeds where more frames need to be generated and inserted between the regular “real-time, master” frames.

This two-mode system ensures that slow-motion feels natural and “sticky” at first, but avoids becoming static and boring by introducing new, deterministically generated content during extreme time-stretches.

The LOD System and Features

In broad terms these information include:

• LOD 0
  • What is the current random value? randVal
• LOD 1
  • Is the current value different from the frame before? has_changed
  • What is the value at the previous frame? randVal_previous
• LOD 2
  • How far along am I in this hold period? hold_progress
  • What was the frame number of the last jump? last_changed_frame
  • What is the frame number of the upcoming jump? next_changed_frame
  • What will be the random value of the next hold? randVal_next_changed_frame
  • For QS only
    • What are the raw values of stream 1 and stream 2? randStreams
    • Which is the currently selected stream? selected_stream_idx

LOD 2’s Search Feature - Time Traveling

The higher computational cost of LOD 2 is due to its robust, stateless search. The process of “searching through time” is to iteratively look ahead to find next_changed_frame and last_changed_frame.

To do this, the wrapper performs a two-phase search (an exponential probe followed by a binary search) by recursively calling the base algorithm at LOD 0. This stateless “discovery” method is what guarantees accuracy without relying on memory or state, but it requires re-calculating values for surrounding frames.

Obtaining next_changed_frame and last_changed_frame unlocks the following:

• randVal_next_changed_frame the random value at the next jump.
• hold_progress can be evaluted, expressed as a normalised value

Wrapper Version Conclusion

These enhancements enable meaningful analysis of FPS-R outputs for transparency, traceability and auditable workflows.

fpsr_tech.md Read more about the technical detail of each algorithm here.

---

Fields of Applications

FPS-R describes a fundamental and observable phenomenon found across many fields. As such, it can be applied to almost any area to inject complexity and non-linearity.

fpsr_applications.md A more comprehensive document detailing potential areas of application.

• Realism and Naturalistic Behaviour
  • robotics, including more natural human-like movement, deliberation, hesitation, pauses, and intentionality.
  • swarm behaviour in drones
  • games eg. unpredictable NPC behaviour, enemy patterns, conversational branches, etc.
  • animation and visualisation,
    • when used in temporal domain, more natural and complex timing and phrasing
    • when used in spatial domains, it increases non-repeating procedural visual detail
  • breaking out of logic loops, eg. a robot vacuum cleaner stuck in a circuitous loop, with injected randomness in each loop
• Organic Unpredictability
  • analogue circuit emulation
  • invoking chat agent attention drift
  • non-linear shifts in conversation topics, intentional (slightly) off-topic diversions
  • intentional wandering in AI inferences can introduce neighbouring topics in an unexpected but controlled manner. These moments of organic divergence may spark creativity and lead to “light-bulb moments.”
• Cryptography and Compression
  • introducing controlled randomness (negentropy) into file signatures to enhance compression efficiency
  • creating non-linear ciphers and keys that are not purely random, random values that hold is a surprise in itself
• Cybersecurity
  • Timing in protocols:
    • Authentication. By introducing a stateless and deterministic time factor into authentication protocols, we add an extra layer of protection.
    • Channel Hopping behaviour. By introducing a stateless, auditable, and deterministic synchronised hopping pattern in the temporal domain, security complexity is increased.
• Strategic, Simulation, Observation
  • Model Complex Systems with High Fidelity: Emulate the non-linear dynamics of large-scale systems across diverse scenarios—from the emergent effects of economic policy to the complex behaviors in science, finance, military, and artificial intelligence.
  • Inject Realistic, Multi-Scale Decision-Making: FPS-R excels at modeling the nuanced, human-like decision frameworks within these systems. It can drive agent behavior at every level, from high-level strategic choices down to the actions of individuals. By introducing realistic deliberation, delayed adoption, and hesitation, simulations can reveal complex emergent phenomena that realistically mirror real-world systems.
  • Unlock Powerful Analytical Benefits: The “glass-box” nature of FPS-R provides unique advantages for observation and analysis:
    • Effortless “What-If” Exploration: Instantly explore alternate timelines and test different strategies simply by adjusting seeds and parameters, without altering the core logic of the simulation.
    • Complete Traceability: Every event and decision is fully auditable and repeatable, allowing complex processes to be studied and understood in granular detail.
    • Efficient Hybrid State Management: Revolutionise how simulation data is handled by drastically reducing data logging overhead. While the simulation’s cumulative, stateful values (e.g., population count, resource levels) must still be logged, FPS-R eliminates the need to log the countless underlying temporal events and non-stateful decisions that lead to those outcomes. They can be perfectly regenerated from a concise set of keys and time-steps, allowing for detailed analysis without extensive storage.
  • Digital Twin Systems
    • Emulate timing realism to capture the true dynamics of physical environments with asynchronous components or variable latency.
    • Reveal edge-case behaviours, coordination failures, and emergent anomalies through expressive timing.
    • Transform digital twins into living diagnostic tools capable of:
      • Stress-testing resilience.
      • Training adaptive responses.
      • Identifying vulnerabilities caused by timing issues.
  • Reality modeling (advanced application).
    • For a historical event that has a recorded history of occurrences, if we can find a set of FPS-R parameters and seed that closely matches the timing of occurrences (temporal fit) and intensity (output value fit) of the event
      • we can extend the timeline (look into the future and the past) of this matching timeline and extrapolate the FPS-R signals to model a probable future, or probable futures for n number of next closest matches.
      • Historical data fitting and predictive modelling can be applied to:
        • Economics, Climate Science, Epidemiology, Finance and Social Sciences

fpsr_applications.md A more comprehensive document detailing potential areas of application.

---

Future Expansion: Capsules

Capsules as Building Blocks of FPS-R

A Capsule is a self-contained, portable data structure that encapsulates a complete FPS-R “performance.” Think of it as a preset or a clip. Each Capsule stores:

• The Algorithm: Which FPS-R algorithm to use (SM, TM, or QS).
• The Parameters: The full set of parameters that define the algorithm’s unique behavior.
• The Duration: A defined start and end frame, giving the performance a specific length.

Essentially, a Capsule is a single, reusable “block” of deterministic, non-linear behavior, storing “presets” and “performances” similar to audio or video clips.

This is where the power of Capsules becomes clear. If a single Capsule is a “word” or a musical “note,” then you can arrange them to create sophisticated compositions.

The Timeline: Capsules can be placed sequentially on a “timeline” or a “playlist.” By stringing together different Capsules—like cautious_hesitation.cap followed by erratic_burst.cap—you can build complex behavioral narratives for an AI, a robot, or an animation.

A True Grammar: This system transforms FPS-R from a raw generator into a true compositional language. You are no longer just sculpting a single, continuous stream; you are arranging discrete ideas into phrases, sentences, and stories. This unlocks nuanced complex and even layered behaviours. Now imagine a natural extension of a single timeline into simultaneous multi-track, multi-channel timelines with clips running in parallel, adding and subtracting from each other. This can create meaningful complexity that unlocks deeper expressivity.

Powerful Application Examples: Security and Obfuscation

• Time-Based Passphrases: A specific sequence of Capsules on a timeline can act as a complex, dynamic key. A system could require a match not just for a single value, but for an entire “performance” across thousands of frames, making it incredibly difficult to crack. The sequence capsule_A -> capsule_C -> capsule_B is a completely different “passphrase” from capsule_B -> capsule_A -> capsule_C.
• Multi-Layered Obfuscation: This is where it becomes truly elegant. You can introduce a global “secret offset” that modifies the seeds of every Capsule on the timeline.
  • The “soul” of the performance—the specific algorithms, their parameters, and their relative timing—remains identical.
  • The “signal”—the actual random values produced—changes completely.

This creates a powerful, two-factor system. To unlock the content, an adversary would need not only the correct sequence of Capsules (the timeline) but also the correct secret offset. This provides multiple, independent layers of obfuscation behind a veil of deterministic complexity.

The applications of expressive phrases of auditable, traceable and controllable performances of stateless, deterministic random hold and jump are wide and diverse. And in the centre of it, FPS-R as the foundational grammar.

---

Conclusion

FPS-R is more than a pseudo-random number stream generator; it is a meticulously designed framework that fills a critical gap between chaotic randomness and rigid predictability. By providing a stateless, deterministic, and mathematically pure way to model the “hold-and-jump” phenomena found throughout nature, it offers a new, foundational primitive for a vast array of applications.

Beyond being a technical primitive, FPS-R is a new lens for observing, expressing and composing with the grammar of our non-linear world.

From building more believable AI and resilient systems to composing complex security protocols with Capsules, FPS-R provides the tools to move beyond simple emulation and toward true, expressive composition. It is a “glass-box” framework designed for exploration, precision, and scalability, inviting developers, researchers, and creators to harness the power of predictable unpredictability.

The potential for composability enables FPS-R to combine its time-phrased output in numerous ways. Moving forward, the vision for capsules allows for the encapsulation of performance clips that capture different “moods” across an infinite timeline, utilising various parameter combinations. This further unlocks richer and deeper “move and hold” phrases, enabling a new form of expressiveness that communicates with true non-linearity.

Join me in exploring the limitless possibilities of FPS-R. Together, we can shape the future of non-linear composition with creativity!

---

Other Documents

Supplementary documents referenced.

fpsr_tech.md Technical docs showing the math logic and code for all the algorithms.

fpsr_applications.md A more comprehensive document detailing potential areas of application.

fpsr_unifying_theory.md A philosophical exploration of surprise, examining nature’s complexity and non-linearity, and how FPS-R captures this essence to enhance simulations and emulations with natural complexity.

Origins, Journals and Reflections A record of my development journey, including inspirations and challenges encountered along the way.

fpsr_algoAnalysis A Jupyter notebook with data graph plots for interactive exploration and experimentation. Try it out yourself!

README-CH The Chinese version of this document.

This site is open source. Improve this page.